Do machines speak? Audio fingerprinting of internal combustion engines
On a cold winter morning in December 2021 in the Solita Research R&D group we packed our bags with various audio recording equipment and set our sights on a local industrial machine rental company. We wanted to answer a simple question: do machines speak? Our aim was to record sound from multiple identical industrial grade machines (which turned out to be 53 kg soil compactors) in order to investigate whether we could consistently distinguish them based on their sound alone. In other words, just as each human has a very unique voice, our hypothesis was that the same would be true for machines, that is, we wanted to construct an audio fingerprint. This could then be used not only to identify each machine, but to detect if a particular machine’s sound starts to drift (indicating a potential incoming fault) or to check whether the fingerprint matches before and after renting out the machine, for example.
It is always important to keep the business use case and real-world limitations in mind when designing solutions to data-based (no pun intended) problems. In this case, we identified the following important aspects in our research problem:
- The solution would have to be lightweight, capable of being run on the edge with limited computational resources and internet connectivity.
- Our methods should be robust against interference from varying levels of background noise and variances in how users hold the microphone when recording a machine’s sound.
- It would be important to be able to communicate our results and analysis to domain experts and eventual end users. Therefore, we should focus on physically meaningful features over arbitrary ones and on explainable algorithms over black boxes.
- The set-up of our experiment should be planned to ensure high-quality uncontaminated data that at the same time would serve to produce the best possible research outcome while being representative of the data we might expect for a productionalised solution.
In this blog post we will focus on points 1. and 3. and we’ll return to 2. and 4. in a follow-up post.
Analysing Sound
We are surrounded by a constant stream of sound mixed together from a multitude of sources: cars speeding along on the street, your colleague typing on their keyboard or a dog barking at songbirds outside your window. Yet, seemingly without any effort, your brains can process this jumbled up signal and tell you exactly what is happening around you in real-time. Our hope is that we could somehow imitate this process by developing audio analysis methods with similar properties.
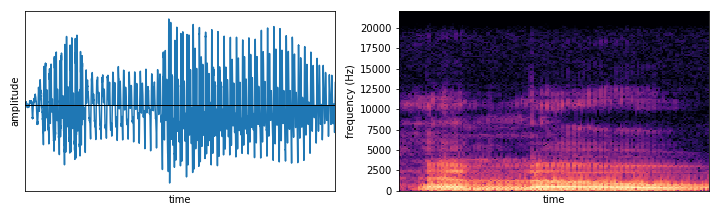
It is quite futile to try to analyse raw signals of this type directly: each sound source emits vibrations in multiple frequencies and these get combined over all the different sources into one big mess. Luckily there is a classical mathematical tool which can help us to figure out the frequency content of an audio (or any other type) wave: the Fourier transform. By computing the Fourier transform for consecutive small windows of the input signal, we can determine how much of each frequency is present at a given time. We can then arrange this data in the form of a matrix, where the rows correspond to different frequency ranges and columns are consecutive time steps (typically in the order of 10-20 milliseconds each). Hence, the entries of the matrix tell you how much of each frequency is present at that particular moment. The resulting matrix is called a spectrogram, which we can visualise by colouring the values based on their magnitudes: dark for values close to zero with lighter colours signifying higher intensity. In Figure 1 you can see an example of the waveform produced by the author uttering “hello” and the resulting spectrogram. The process of transforming the original signal to its constituent frequencies and studying this decomposition is called spectral analysis.
From Raw to Refined Features
The raw frequency data by itself is still not the most useful. This is because different audio sources can of course produce sounds in overlapping frequency ranges. In particular, a single machine can have multiple vibrating parts which each produce their distinct sound. Instead, we should try to extract features that are meaningful to the problem at hand—classification of fuel powered machines in this case. There are many spectral features that could be useful (for some inspiration you can check out our public Google Colab notebooks or the documentation of librosa, a popular Python audio analysis library).
In this blog we’ll take a slightly different approach. Our goal is to be able to compare the frequency data of different machines at two points in time, but this won’t be efficient (let alone robust) if we rely on raw frequencies. This is because of background noise and the varying operating speed of the engines (think about how the pitch of the sound is affected by how fast the engine is running). Instead, we want to pool together individual frequencies in a way that would allow us to express our high-dimensional spectrogram in terms of a handful of distinct frequency range combinations.
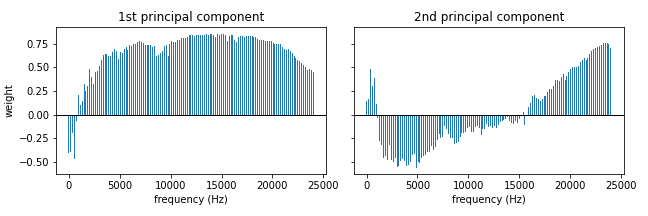
Luckily there is, yet again, a classical mathematical tool which does exactly this: principal component analysis (PCA). If you’ve taken a course in linear algebra then this is nothing more than matrix diagonalisation, but it has become one of the staple methods of dimensionality reduction in the machine learning world. The output of the PCA-algorithm is a set of principal components each of which is some combination of the original frequencies. In Figure 2 we plot the weight of each frequency for two principal components: in the first component we have positive weights for all but the lowest of frequencies while for the second one the midrange has negative weights. An additional reason for why PCA is an attractive method for our problem is that the resulting frequency combinations will be linearly independent (i.e. you cannot obtain one component by adding together multiples of the other components). This is a crude imitation of our earlier observation that a single machine can have multiple separate parts producing sound at the same time. The crux of the algorithm is that in order to faithfully represent our original data, we only have to keep a small number of these principal components thus effectively reducing the dimensionality of our problem to a more manageable scale.
Structure in Audio
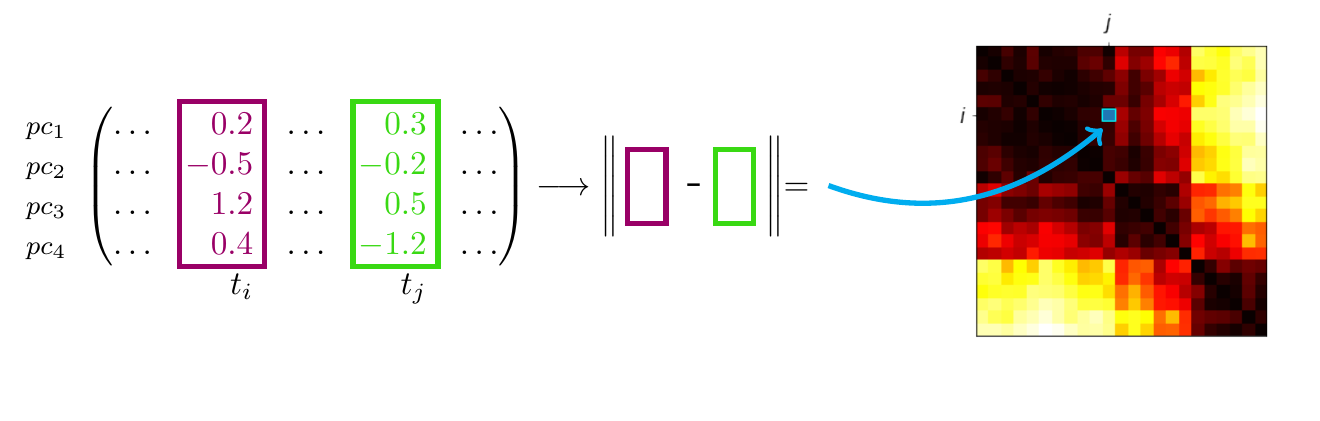
Now that we have a sequence of low-dimensional feature vectors that capture the most important aspects of the original signal, we can try to start finding some structure in this stream of data. We do this by computing the self-similarity matrix (SSM) [1], whose elements are the pairwise distances between our feature vectors. We can visualise the resulting matrix as a heat map where the intensity of the colour corresponds to the distance (with black colour signifying that the features are identical), see Figure 3.
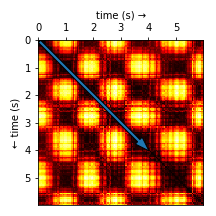
In Figure 4 you can see a part of an SSM for one of the soil compactors. By definition, time flows along its main diagonal (blue arrow). Short segments of the audio that are self-similar (i.e. the nature of the sound doesn’t change) appear as dark rectangles along the diagonal. For each rectangle on the main diagonal, the remaining rectangles on the same row show how similar the other segments are to the one in question. If you pause here for a moment and gather your thoughts, you might notice that there are two types of alternating segments (of varying duration) in this particular SSM.
Do machines speak?
We have covered a lot of technical material, but we are almost done! Now we understand how to uncover patterns in audio, but how can we use this information to tell apart our four machines? The more ML-savvy readers might be tempted to classify the SSMs with e.g. convolutional neural networks. This might certainly work well, but we would lose sight of one of our aims which was to keep the method computationally light and simple. Hence we proceed with a more traditional approach.
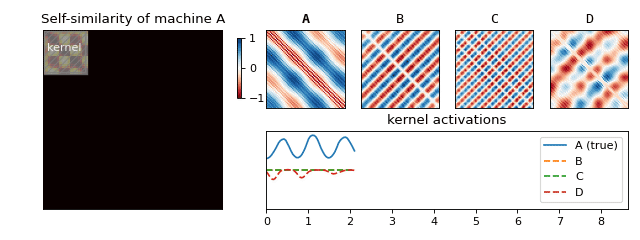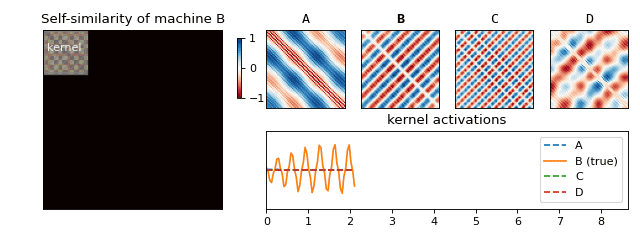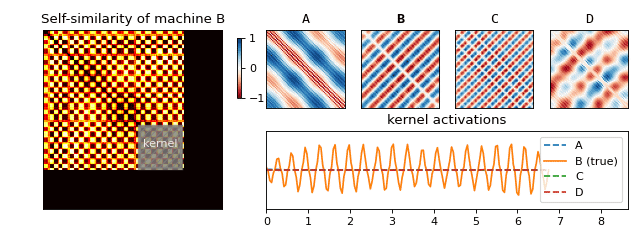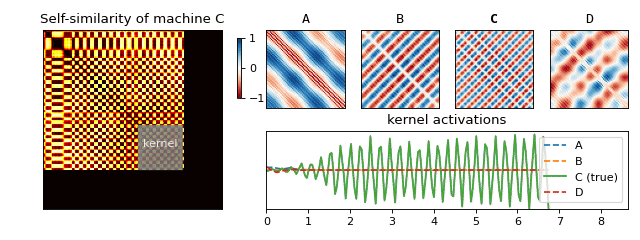
Recall that we have constructed a separate SSM for each machine. For each of the resulting matrices, we can now look at small blocks along the diagonal (see Figure 5) and figure out what they typically look like. If we scale the results to [-1, 1], we obtain a small set of fingerprints (we also refer to these as kernels) for each machine. Just like you (hopefully) have ten fingers each with its own unique fingerprint, a machine can also have more than one acoustic fingerprint. We have visualised a few of these for one of the machines in Figure 5.
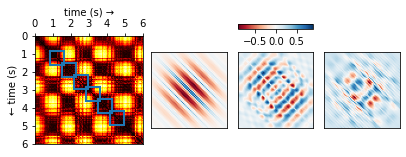
We are now ready to return back to the machine rental shop to test if our solution works! Once we arrive, we follow the set of instructions below in order to determine which machine is which (see Figure 6 for an animation of this process):
- Turn on the machine and record its sound.
- While the machine is running, compute the self-similarity matrix on the fly.
- Slide the fingerprints for each machine along the diagonal and compute their activations (by summing the elementwise product).
- The fingerprint which reacts to the sound the most tells you which machine is running.
And that’s it! We saw how something seemingly natural, the sounds surrounding us, can produce very complex signals. We learned how to begin to understand this mess via spectral analysis, which led us to uncover structure hidden in the data—something our brain does with ease. Finally, we used this structure to produce a solution to our original business use case of classifying machine sounds.
I hope you have enjoyed this little excursion into the mathematical world of audio data and colourful graphs. Maybe next time you start your car (or your soil compactor) you might wonder whether you could recognise its sound from your neighbour’s identical one and what it is about their sounds that lets your brain achieve that.
If you are interested in applying advanced sensor data (audio or otherwise) analytics in your business context please reach out to me or the Solita Industrial team.
References
[1] J. Foote, Visualizing Music and Audio using Self-Similarity, MULTIMEDIA ’99, pp. 77-80 (1999) http://www.musanim.com/wavalign/foote.pdf